前回からの続きです。
- 4つの数と3つの四則演算(×÷+−)を組み合わせて、答えが10になるような計算式を作れ。
- 数字、演算ともに重複あり。
- 単一の負符号はなし。
 GitHub hanepjiv/make10_hsでソースコードを公開しています。
GitHub hanepjiv/make10_hsでソースコードを公開しています。
実装の解説
使用した言語拡張機能
{-# LANGUAGE ScopedTypeVariables
, OverloadedStrings
, GADTs
, Safe
#-}各ソースコードの最初に上記を指定しています。
- ScopedTypeVariables
- 型変数の変換を文脈通りに行ないます。
- OverloadedStrings
- 文字列リテラルを Text, ByteString として扱います。
- GADTs (Generalized algebraic datatypes)
- データ型宣言時に型指定を可能にします。
- Safe
- 言語機能をセキュアな機能のみに限定することを指定し、 セキュアであることを外部(ライブラリを使用する側)に宣言します。
スタイル
Haskellには、do記法とモナドを利用したスタイル以外にもスタイルがあります。
今回は、ArrowスタイルやApplicativeスタイルを使って、 できるだけdo記法を使わないスタイルで書いています。 ただし、Arrow記法は使ってません。
この選択には、あまり理由はありません。
内部表現形式定義
make10 を解くために、内部表現形式を定義します。
演算子 (Operator) を定義する
演算子は(×, ÷, +, −)の4つですが、割り算と引き算は可換ではないので、専用の演算子を考えます。 よって、合計6つの演算子を定義します。
Show クラスから派生させて、数学記号で表示されるように定義しておきます。
src/Game/Make10/Operator.hs
data Operator = ADD
| SUB
| RSUB
| MUL
| DIV
| RDIV
deriving (Bounded, Eq, Ord, Enum)
-- -----------------------------------------------------------------------------
instance Show Operator where
show ADD = " + "
show SUB = " - "
show RSUB = " -< "
show MUL = " * "
show DIV = " / "
show RDIV = " /< "演算子の関数を定義する
演算子を数字に適用したときに、実際に行われる計算を定義します。
RSUB, RDIVは引数を逆順に適用するため、flip関数を利用します。
前回も説明しましたが、 %は、剰余(mod)ではなく、分母を示しています。
src/Game/Make10/Operator.hs
-- | function
--
-- >>> function ADD (1 % 1) 2
-- 3 % 1
--
-- >>> function SUB (1 % 1) 2
-- (-1) % 1
--
-- >>> function RSUB (1 % 1) 2
-- 1 % 1
--
-- >>> function MUL (1 % 1) 2
-- 2 % 1
--
-- >>> function DIV (1 % 1) 2
-- 1 % 2
--
-- >>> function RDIV (1 % 1) 2
-- 2 % 1
--
function :: (Fractional a) => Operator -> a -> a -> a
function ADD = (+)
function SUB = (-)
function RSUB = flip (-)
function MUL = (*)
function DIV = (/)
function RDIV = flip (/)数式 (Cell) を定義する
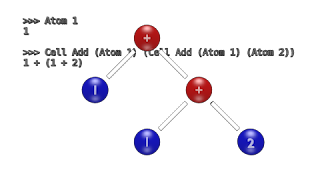
数式はCellと名付けました。 その表現方法は、「数字(Atom)」もしくは「演算子と数式2つの組(Triple)」になります。
TripleがCellを再起的に含んでいるので、式の順番を入れ子で表現できます。
data定義は、GADTs形式で宣言しています。 関数と同じ記法でデータコンストラクタが記述できるので便利です。
src/Game/Make10/Cell.hs
-- | Cell
--
-- >>> Atom (1 % 1)
-- 1 % 1
--
-- >>> Triple Op.ADD (Atom (1 % 1)) (Atom 2)
-- 1 % 1 + 2 % 1
--
-- >>> :{
-- Triple Op.ADD
-- (Atom 1) (Triple Op.ADD (Atom $ 1 % 2) (Atom $ 2 % 3))
-- :}
-- 1 % 1 + (1 % 2 + 2 % 3)
--
data Cell a where
Atom :: a -> Cell a
Triple :: !Op.Operator -> Cell a -> Cell a -> Cell aapply(適用) と eval(評価)
数式を評価して結果の値を計算します。
数字(Atom)を評価すると、そのままの数字が戻ります。
数式を評価すると、右左2つの Cell を評価し、その結果に演算子を適用します。
src/Game/Make10/Cell.hs
apply :: forall a.
(Show a, Fractional a, Eq a) =>
Op.Operator -> Cell a -> Cell a -> Either String a
apply op@Op.RDIV l r = apply (Op.swap op) r l
apply op@Op.DIV l r =
case eval r of
l_@(Left _) -> l_
r_@(Right x) -> if 0 == x
then Left $ "ERROR!: apply: zero divide: " ++ show r
else Op.function op <$> eval l <*> r_
apply op l r = Op.function op <$> eval l <*> eval reval :: forall a.
(Show a, Fractional a, Eq a) =>
Cell a -> Either String a
eval (Atom x) = Right x
eval (Triple op l r) = apply op l r展開形 (Expand) を定義する
同型の数式を排除するために、数式を展開して、項を規則にしたがって並べ替えた状態で比較します。
data Expand a where { ExpandList :: [a] -> Expand a
; ExpandTuple :: ([a], [a]) -> Expand a
} deriving (Eq, Ord, Show)Cell から Expand に変換するわけですが、この過程で除算に対応するために、ExpandTuple が必要になります。項のリストを分母分子で表現して取り回しています。
数式の組み合わせ
与えられた4つの数字で作成できる全ての数式の組み合わせをチェックすれば、解が求められます。
数式の組み合わせの形は、下図の2パターンになります。
赤が演算子、青が数字です。


数え上げ
重複を考慮して、PatternAが12種、PatternBが3種の15種類を調べています。
-- | make_M_4_Triple
--
make_M_4_Triple :: forall a.
(Show a, Ord a, Fractional a) =>
[a] -> [Operator] -> [Cell a]
make_M_4_Triple ns os =
filter (not . hasZeroDiv) (map (gen make_M_4_Triple_A ns os) patternA ++
map (gen make_M_4_Triple_B ns os) patternB)
where
-- -------------------------------------------------------------------------
gen :: forall t a0 a1.
(a0 -> a0 -> a0 -> a0 -> a1 -> a1 -> a1 -> t)
-> [a0] -> [a1] -> [Integer] -> t
gen make_ n_ o_ i_ = make_
(n_ !! fromInteger (head i_))
(n_ !! fromInteger (i_ !! 1))
(n_ !! fromInteger (i_ !! 2))
(n_ !! fromInteger (i_ !! 3))
(head o_)
(o_ !! 1)
(o_ !! 2)
-- -------------------------------------------------------------------------
make_M_4_Triple_A :: forall a0.
a0 -> a0 -> a0 -> a0
-> Operator -> Operator -> Operator -> Cell a0
make_M_4_Triple_A n0 n1 n2 n3 o0 o1 o2 =
Triple o2 (Triple o1 (Triple o0 (Atom n3) (Atom n2)) (Atom n1)) (Atom n0)
-- -------------------------------------------------------------------------
make_M_4_Triple_B :: forall a0.
a0 -> a0 -> a0 -> a0
-> Operator -> Operator -> Operator -> Cell a0
make_M_4_Triple_B n0 n1 n2 n3 o0 o1 o2 =
Triple o2 (Triple o1 (Atom n3) (Atom n2)) (Triple o0 (Atom n1) (Atom n0))
-- -------------------------------------------------------------------------
patternA = [ [0, 1, 2, 3]
, [0, 2, 1, 3]
, [0, 3, 1, 2]
, [1, 0, 2, 3]
, [1, 2, 0, 3]
, [1, 3, 0, 2]
, [2, 0, 1, 3]
, [2, 1, 0, 3]
, [2, 3, 0, 1]
, [3, 0, 1, 2]
, [3, 1, 0, 2]
, [3, 2, 0, 1]
]
-- -------------------------------------------------------------------------
patternB = [ [0, 1, 2, 3]
, [0, 2, 1, 3]
, [0, 3, 1, 2]
]
-- -----------------------------------------------------------------------------
-- | make_M_4
--
make_M_4 :: forall a.
(Show a, Ord a, Fractional a) =>
a -> [a] -> [Cell a]
make_M_4 n a_in =
unseen [optimize t | t <- concatMap (make_M_4_Triple a_in) $
replicateM (pred (length a_in)) allOp
, isRightTrue $ (== n) <$> eval t
]
where
-- -------------------------------------------------------------------------
isRightTrue :: forall t. Either t Bool -> Bool
isRightTrue (Right True) = True
isRightTrue _ = False
-- -------------------------------------------------------------------------
unseen :: forall a0. (Ord a0, Num a0) => [Cell a0] -> [Cell a0]
unseen [] = []
unseen x_ = unseen_ x_ Set.empty
where
unseen_ :: forall a1. (Ord a1, Num a1) =>
[Cell a1] -> Set.Set (Game.Make10.Expand.Expand a1)
-> [Cell a1]
unseen_ [] _ = []
unseen_ (x:xs) seen = unseen__ x xs seen $! expand x
where
unseen__ x__ xs__ seen_ e
| e `Set.member` seen_ = unseen_ xs__ seen_
| otherwise = x__ : unseen_ xs__ (Set.insert e seen_)──続きます。
0 件のコメント:
コメントを投稿